Master the 2 Sample Z Proportion Test Easily
<!DOCTYPE html>
Are you struggling to compare proportions between two groups? The 2 Sample Z Proportion Test is a powerful statistical tool that can help you determine if there’s a significant difference between two population proportions. Whether you’re a student, researcher, or data analyst, mastering this test will enhance your ability to draw accurate conclusions from data. In this guide, we’ll break down the process step-by-step, making it easy to understand and apply. (2 sample z proportion test, statistical significance, comparing proportions)
What is the 2 Sample Z Proportion Test?

The 2 Sample Z Proportion Test is a hypothesis test used to compare the proportions of two independent groups. It helps determine if the difference between the observed proportions is statistically significant or due to random chance. This test is widely used in fields like marketing, healthcare, and social sciences. (hypothesis testing, independent groups, statistical significance)
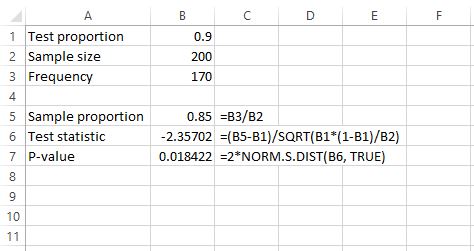
When to Use the 2 Sample Z Proportion Test

Before diving into the test, ensure it’s the right tool for your data. Use this test when:
- You’re comparing two independent groups.
- The data is categorical (e.g., yes/no, success/failure).
- The sample sizes are large enough (generally, both groups should have at least 10 successes and 10 failures).
📊 Note: Ensure your data meets these conditions for accurate results. (categorical data, sample size requirements, independent groups)
Step-by-Step Guide to Performing the 2 Sample Z Proportion Test
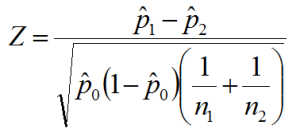
Step 1: State the Hypotheses
Begin by defining the null and alternative hypotheses:
- Null Hypothesis (H₀): The proportions are equal (p₁ = p₂).
- Alternative Hypothesis (H₁): The proportions are not equal (p₁ ≠ p₂) or one proportion is greater/less than the other (p₁ > p₂ or p₁ < p₂).
Step 2: Calculate the Pooled Proportion
The pooled proportion (p̂) is the weighted average of the sample proportions:
[ \hat{p} = \frac{x_1 + x_2}{n_1 + n_2} ]
Where ( x_1 ) and ( x_2 ) are the number of successes in each group, and ( n_1 ) and ( n_2 ) are the sample sizes. (pooled proportion, sample proportions, weighted average)
Step 3: Compute the Test Statistic
The test statistic (Z) is calculated using the formula:
[ Z = \frac{(\hat{p}_1 - \hat{p}_2)}{\sqrt{\hat{p}(1 - \hat{p}) \left( \frac{1}{n_1} + \frac{1}{n_2} \right)}} ]
Where ( \hat{p}_1 ) and ( \hat{p}_2 ) are the sample proportions of each group. (test statistic, z-score, standard error)
Step 4: Determine the P-Value
Compare the calculated Z-score to the standard normal distribution to find the p-value. A p-value less than your significance level (commonly 0.05) indicates a significant difference. (p-value, significance level, standard normal distribution)
Step 5: Make a Decision
Reject the null hypothesis if the p-value is less than the significance level. Otherwise, fail to reject it. (hypothesis testing, decision-making, statistical significance)
Checklist for Performing the 2 Sample Z Proportion Test
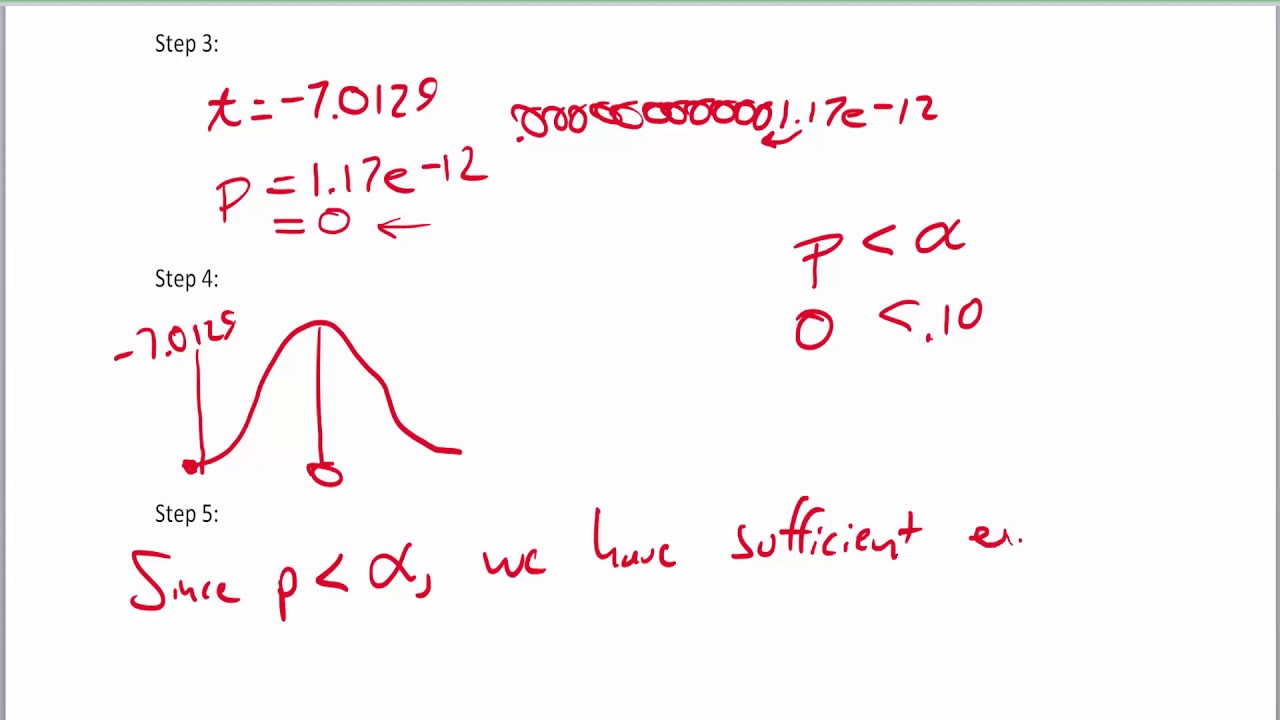
- Verify the data meets the test conditions.
- State the null and alternative hypotheses.
- Calculate the pooled proportion.
- Compute the test statistic (Z-score).
- Determine the p-value and compare it to the significance level.
- Make a decision based on the p-value. (checklist, hypothesis testing, p-value)
Mastering the 2 Sample Z Proportion Test is essential for anyone working with categorical data. By following these steps, you can confidently compare proportions and draw meaningful insights from your data. Whether you’re analyzing survey results or clinical trial data, this test is a valuable tool in your statistical toolkit. (categorical data, hypothesis testing, statistical insights)
What is the 2 Sample Z Proportion Test used for?
+It’s used to compare the proportions of two independent groups to determine if the difference is statistically significant. (comparing proportions, statistical significance, independent groups)
What are the assumptions of the 2 Sample Z Proportion Test?
+The test assumes independence of samples, categorical data, and sufficient sample sizes (at least 10 successes and failures in each group). (assumptions, categorical data, sample size)
How do I interpret the p-value in this test?
+A p-value less than the significance level (e.g., 0.05) indicates a significant difference between the proportions. (p-value, significance level, interpretation)


