Angles Inside Circle Theorem: Essential Geometry Insights
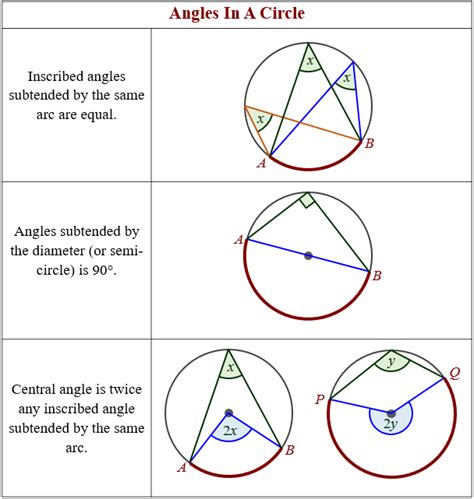
Understanding the Angles Inside Circle Theorem is crucial for anyone delving into geometry. This theorem not only simplifies complex problems but also lays the foundation for advanced mathematical concepts. Whether you're a student, educator, or geometry enthusiast, mastering this theorem will enhance your problem-solving skills and deepen your appreciation for the elegance of circles and angles. (circle theorems, geometry insights, angles in circles)
What is the Angles Inside Circle Theorem?

The Angles Inside Circle Theorem states that the angle subtended by an arc at the center of a circle is twice the angle subtended by the same arc at any point on the circumference. This fundamental principle is a cornerstone in geometry, connecting angles, arcs, and circle properties seamlessly. (circle properties, angle subtended by arc, geometry theorems)
Key Applications of the Theorem

This theorem has wide-ranging applications, from solving geometric proofs to designing architectural structures. Here are some practical uses:
- Geometric Proofs: Simplify complex proofs involving circles and angles.
- Engineering Design: Apply the theorem in designing curved structures like bridges and domes.
- Art and Graphics: Use it to create symmetrical and balanced designs.
📘 Note: Always ensure the arc and angles are clearly defined when applying this theorem.
Steps to Apply the Angles Inside Circle Theorem

Follow these steps to effectively use the theorem:
- Identify the Arc: Determine the arc subtending the angles.
- Locate the Center: Find the center of the circle.
- Measure Angles: Measure the angle at the center and the circumference.
- Apply the Theorem: Use the relationship to find the unknown angle.
(geometric steps, applying circle theorems, angle measurement)
Common Mistakes to Avoid
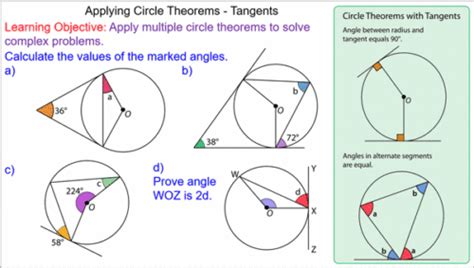
When working with the Angles Inside Circle Theorem, avoid these pitfalls:
- Confusing the center angle with the circumference angle.
- Ignoring the arc’s role in determining angles.
- Misapplying the theorem to non-circular shapes.
(common geometry mistakes, theorem application tips, circle theorem errors)
Comparison of Angles in Circles
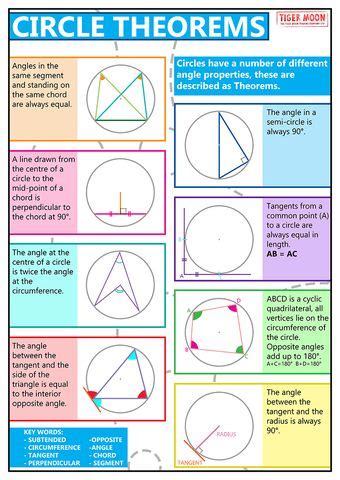
| Type of Angle | Location | Relationship |
|---|---|---|
| Central Angle | Center of Circle | Twice the inscribed angle |
| Inscribed Angle | Circumference | Half the central angle |

(angle comparison, central vs inscribed angle, circle angle relationships)
The Angles Inside Circle Theorem is an indispensable tool in geometry, offering clarity and precision in solving problems related to circles and angles. By understanding its principles and applications, you can tackle complex geometric challenges with confidence. Remember to practice regularly and avoid common mistakes to master this theorem effectively. (geometry mastery, circle theorem practice, angles in circles)
What is the Angles Inside Circle Theorem?
+
It states that the angle subtended by an arc at the center of a circle is twice the angle subtended by the same arc at any point on the circumference.
How is this theorem applied in real life?
+
It’s used in engineering, architecture, and art to design curved structures and symmetrical patterns.
What are common mistakes when using this theorem?
+
Common mistakes include confusing center and inscribed angles, ignoring the arc, and misapplying the theorem to non-circular shapes.



