Mastering Angles Outside a Circle: Key Geometry Insights
Mastering angles outside a circle is a crucial skill in geometry, offering insights into relationships between lines, circles, and angles. Whether you're a student preparing for exams or a professional applying geometric principles, understanding these concepts can significantly enhance your problem-solving abilities. This guide breaks down the key principles, providing clear explanations and practical tips to help you grasp angles outside a circle with ease. From theorems to real-world applications, we’ve got you covered. (geometry principles, angles in circles, geometric theorems)
Understanding Angles Outside a Circle: The Basics
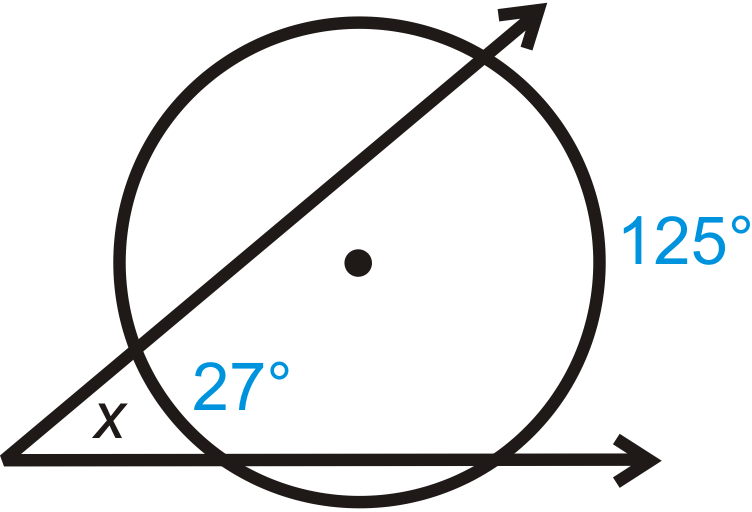
Angles outside a circle, often referred to as exterior angles, are formed when a tangent and a secant or two secants intersect outside the circle. These angles have unique properties that differentiate them from angles inside or on the circle. Key concepts include the external angle theorem and the relationship between the angle and the intercepted arc. (exterior angles, external angle theorem, intercepted arc)
Key Properties of Exterior Angles
- The External Angle Theorem: The measure of an exterior angle is half the difference of the measures of the intercepted arcs.
- Tangent-Secant Theorem: When a tangent and a secant intersect outside a circle, the measure of the angle formed is half the difference of the intercepted arcs.
- Secant-Secant Theorem: For two secants intersecting outside a circle, the angle measure is half the difference of the intercepted arcs.
Practical Applications and Problem-Solving

Understanding angles outside a circle isn’t just theoretical—it has practical applications in fields like architecture, engineering, and design. Mastering these concepts allows you to solve complex problems efficiently. Below is a step-by-step approach to tackling related geometry questions. (practical geometry, problem-solving in geometry, real-world applications)
Steps to Solve Problems Involving Exterior Angles
- Identify the Elements: Locate the tangent, secant, and intercepted arcs in the diagram.
- Apply the Theorem: Use the external angle theorem or tangent-secant/secant-secant theorem as applicable.
- Calculate the Angle: Substitute the arc measures into the formula to find the angle.
📌 Note: Always double-check the intercepted arcs to ensure accurate calculations.
| Theorem | Formula |
|---|---|
| External Angle Theorem | Angle = ½ × (Difference of Intercepted Arcs) |
| Tangent-Secant Theorem | Angle = ½ × (Difference of Intercepted Arcs) |
| Secant-Secant Theorem | Angle = ½ × (Difference of Intercepted Arcs) |

Mastering angles outside a circle opens up a world of geometric possibilities, from solving intricate problems to applying these principles in real-world scenarios. By focusing on key theorems, practicing regularly, and understanding practical applications, you’ll gain confidence in tackling even the most challenging geometry questions. Remember, consistency is key—keep practicing, and soon, these concepts will become second nature. (geometric mastery, problem-solving skills, geometry practice)
What is the external angle theorem?
+
The external angle theorem states that the measure of an exterior angle is half the difference of the measures of the intercepted arcs.
How do I apply the tangent-secant theorem?
+
Identify the tangent, secant, and intercepted arcs, then use the formula: Angle = ½ × (Difference of Intercepted Arcs).
Where are angles outside a circle used in real life?
+
These principles are applied in architecture, engineering, and design to solve problems involving circular structures and pathways.



