Understanding Simple Cubic Coordination Number: A Quick Guide
Understanding the concept of Simple Cubic Coordination Number is essential for anyone delving into the world of crystal structures and material science. This quick guide will walk you through the basics, applications, and significance of this fundamental concept, ensuring you grasp its importance in both academic and commercial contexts.
What is Simple Cubic Coordination Number?

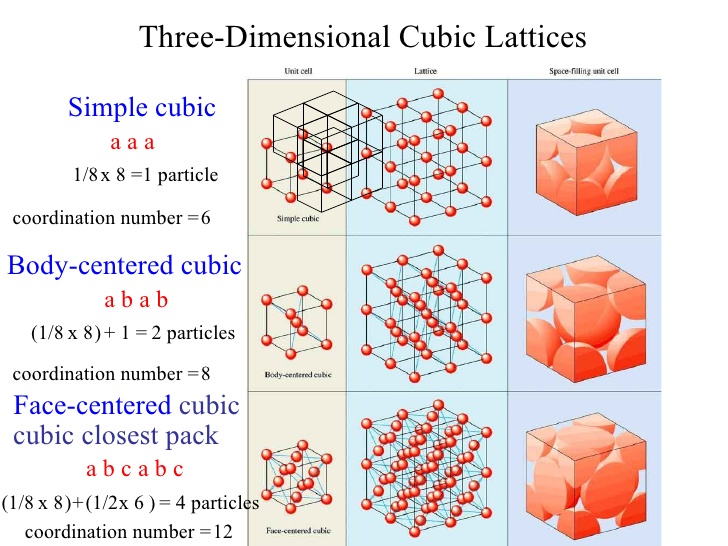
The Simple Cubic Coordination Number refers to the number of nearest neighbors that a central atom or ion has in a simple cubic crystal lattice. In this structure, each atom is located at the corner of a cube, sharing its influence with adjacent atoms. The coordination number in a simple cubic lattice is 6, as each atom is surrounded by six nearest neighbors.
📌 Note: The simple cubic structure is one of the simplest crystal lattices, making it an ideal starting point for understanding more complex arrangements.
Key Features of Simple Cubic Lattice

- Structure: Each atom is positioned at the corner of a cube.
- Coordination Number: 6 nearest neighbors.
- Packing Efficiency: Approximately 52%, which is relatively low compared to other structures.
| Feature | Description |
|---|---|
| Coordination Number | 6 |
| Packing Efficiency | 52% |
| Structure Type | Simple Cubic |

Applications of Simple Cubic Coordination Number

Understanding the coordination number is crucial in various fields, including:
- Material Science: Designing materials with specific properties.
- Nanotechnology: Creating nanostructures with precise atomic arrangements.
- Chemistry: Studying reaction mechanisms and crystal growth.
Commercial Applications
For businesses, knowledge of simple cubic coordination numbers is vital in:
- Manufacturing: Producing materials with consistent properties.
- Research & Development: Innovating new materials and technologies.
- Quality Control: Ensuring product integrity through structural analysis.
How to Calculate Coordination Number

Calculating the coordination number involves identifying the nearest neighbors in a lattice. For a simple cubic structure:
- Visualize the Lattice: Imagine a cube with atoms at each corner.
- Identify Neighbors: Count the atoms directly adjacent to the central atom.
- Sum the Neighbors: In a simple cubic lattice, this number is always 6.
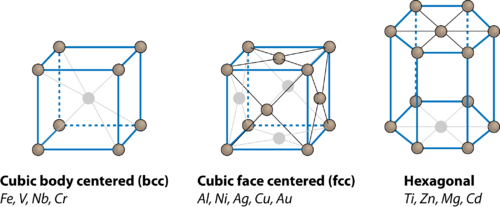
✨ Note: This method applies specifically to simple cubic structures. Other lattices, like face-centered or body-centered cubic, have different coordination numbers.
Checklist for Understanding Simple Cubic Coordination Number
- Define the Concept: Know what coordination number represents.
- Identify the Structure: Recognize the simple cubic lattice.
- Calculate Neighbors: Determine the number of nearest atoms.
- Apply Knowledge: Use this understanding in practical scenarios.
What is the coordination number in a simple cubic lattice?
+The coordination number in a simple cubic lattice is 6, as each atom is surrounded by six nearest neighbors.
Why is the packing efficiency low in simple cubic structures?
+The packing efficiency is approximately 52% because atoms occupy only the corners of the cube, leaving significant empty space within the lattice.
How does coordination number impact material properties?
+Coordination number influences properties like density, conductivity, and reactivity by determining how atoms interact within the material.
In summary, the Simple Cubic Coordination Number is a foundational concept in understanding crystal structures. Its applications span from academic research to commercial innovation, making it a vital topic for both learners and professionals. By mastering this concept, you’ll gain valuable insights into the atomic arrangements that shape materials and technologies. crystal structures,material science,atomic arrangements.



