Understanding the Symmetric Property of Equality

<!DOCTYPE html>
Have you ever wondered why if A = B, then B = A? This fundamental concept in mathematics is known as the Symmetric Property of Equality. It’s a cornerstone in algebra and problem-solving, ensuring consistency and fairness in equations. Whether you’re a student, educator, or simply curious about math principles, understanding this property is essential. Let’s dive into what it means, how it works, and why it matters, along with practical examples and tips for application (mathematical properties, algebra basics, equation solving).
What is the Symmetric Property of Equality?
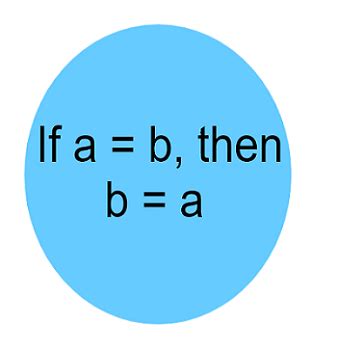
The Symmetric Property of Equality states that if one quantity is equal to another, then the other quantity is also equal to the first. In mathematical terms, if A = B, then B = A. This property ensures that equality is a two-way relationship, not dependent on the order of the quantities (mathematical definitions, equality rules, symmetric property).
Why is the Symmetric Property Important?

This property is crucial because it provides a foundation for logical reasoning in mathematics. It allows us to manipulate equations confidently, knowing that equality remains consistent regardless of the direction. For example, if you know x = 5, you can immediately conclude that 5 = x. This simplicity is powerful in solving complex problems (algebraic reasoning, problem-solving techniques, mathematical logic).
How to Apply the Symmetric Property

Applying the symmetric property is straightforward. Whenever you encounter an equation, remember that you can reverse the equality without changing its truth value. Here’s a step-by-step guide:
- Identify the Equation: Start with an equation like A = B.
- Apply the Property: Reverse the equation to get B = A.
- Verify: Ensure both statements are true and consistent.
📌 Note: This property only applies to equalities, not inequalities (equation manipulation, symmetric property application, mathematical consistency).
Examples of the Symmetric Property in Action
Let’s look at a few examples to illustrate the symmetric property:
| Original Equation | Applied Symmetric Property |
|---|---|
| 7 = x + 3 | x + 3 = 7 |
| y - 2 = 10 | 10 = y - 2 |

These examples show how the property simplifies equation rearrangement (practical examples, symmetric property examples, equation rearrangement).
Common Misconceptions About the Symmetric Property

While the symmetric property is straightforward, there are common misconceptions to avoid:
- Confusing with Transitive Property: The symmetric property deals with reversing equality, while the transitive property involves three quantities (A = B and B = C implies A = C).
- Applying to Inequalities: The symmetric property does not apply to inequalities like A > B.
📌 Note: Always ensure you’re working with equalities when applying this property (common mistakes, mathematical misconceptions, property distinctions).
Checklist for Mastering the Symmetric Property
To master the symmetric property, follow this checklist:
- Understand the definition: If A = B, then B = A.
- Practice reversing equations in simple problems.
- Distinguish between symmetric and transitive properties.
- Apply the property in complex equations to build confidence.
By following these steps, you’ll become proficient in using the symmetric property (mastering mathematics, learning checklist, symmetric property practice).
The Symmetric Property of Equality is a simple yet powerful tool in mathematics. It ensures that equality is bidirectional, allowing us to manipulate equations with confidence. By understanding and applying this property, you’ll enhance your problem-solving skills and mathematical reasoning. Remember, practice makes perfect, so keep exploring examples and challenging yourself. Now that you’re equipped with this knowledge, you’re ready to tackle equations with ease (mathematical confidence, problem-solving skills, equation mastery).
What is the Symmetric Property of Equality?
+The Symmetric Property of Equality states that if A = B, then B = A, ensuring equality is bidirectional.
Can the Symmetric Property be applied to inequalities?
+No, the Symmetric Property only applies to equalities, not inequalities.
How is the Symmetric Property different from the Transitive Property?
+The Symmetric Property reverses equality (A = B implies B = A), while the Transitive Property involves three quantities (A = B and B = C implies A = C).


