Exploring Deterministic Finite Automata: Key Papers

Exploring Deterministic Finite Automata: Key Papers
Deterministic Finite Automata (DFA) are fundamental concepts in computer science, particularly in the study of formal languages and computation. Understanding DFA is crucial for anyone delving into theoretical computer science, compiler design, or even practical applications like text processing. This blog post explores key papers that have shaped the understanding and application of DFA, providing both informative insights and commercial value for readers.
What is a Deterministic Finite Automaton (DFA)?
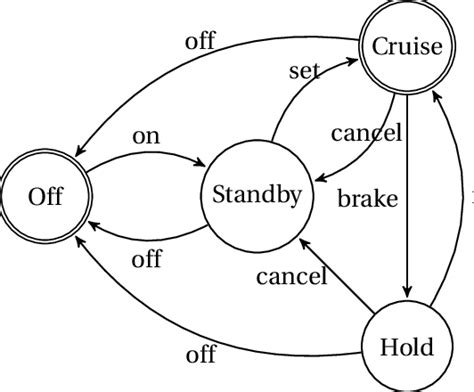
A Deterministic Finite Automaton (DFA) is a theoretical machine that recognizes patterns within input through a finite number of states. It transitions between states based on input symbols, following a deterministic rule. DFAs are widely used in lexical analysis, pattern matching, and string processing.
💡 Note: DFAs are essential in designing compilers and parsers due to their efficiency and simplicity.
Key Papers in DFA Research

1. “Finite Automata and Their Decision Problems” by Michael O. Rabin and Dana Scott (1959)
This seminal paper introduced the concept of finite automata and proved their equivalence to regular expressions. It laid the foundation for automata theory and its applications in formal language recognition.
- Key Contribution: Established the mathematical framework for DFAs.
- Relevance: Essential for understanding the theoretical underpinnings of DFAs.
2. “Introduction to Automata Theory, Languages, and Computation” by John E. Hopcroft, Rajeev Motwani, and Jeffrey D. Ullman (2006)
This textbook, while not a paper, is a cornerstone in automata theory education. It covers DFAs extensively, including their construction, minimization, and applications.
- Key Contribution: Comprehensive guide to DFA theory and practice.
- Relevance: Ideal for students and professionals seeking a deep understanding of DFAs.
3. “Deterministic Finite Automata Minimization Algorithms” by Derick Wood (1973)
Wood’s paper focuses on minimizing DFAs, a critical process to reduce the number of states and improve efficiency. It presents algorithms like the Hopcroft’s algorithm for DFA minimization.
- Key Contribution: Practical algorithms for DFA optimization.
- Relevance: Valuable for developers working on efficient pattern-matching systems.
| Paper | Year | Key Focus |
|---|---|---|
| Rabin & Scott | 1959 | Theoretical Foundations |
| Hopcroft et al. | 2006 | Educational Resource |
| Derick Wood | 1973 | DFA Minimization |

Practical Applications of DFA
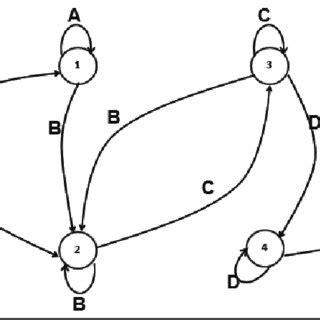
DFAs are not just theoretical constructs; they have real-world applications in:
- Lexical Analysis: Used in compilers to tokenize source code.
- Pattern Matching: Efficiently search for patterns in text.
- Network Protocols: Analyze data packets in real-time.
📌 Note: DFAs are preferred in scenarios requiring deterministic behavior and efficiency.
Checklist for Exploring DFA Papers

- Read Rabin & Scott (1959) for theoretical foundations.
- Study Hopcroft et al. (2006) for a comprehensive overview.
- Explore Wood (1973) for DFA minimization techniques.
- Apply DFA concepts in lexical analyzers or pattern-matching tools.
Wrapping Up

Deterministic Finite Automata are a cornerstone of computer science, with their roots deeply embedded in key papers and textbooks. Whether you’re a student, researcher, or developer, understanding DFAs opens doors to advanced topics in automata theory and practical applications. By exploring the papers highlighted above, you’ll gain both theoretical knowledge and practical skills to apply DFAs effectively.
What is the difference between DFA and NFA?
+A DFA (Deterministic Finite Automaton) has exactly one transition per state for each input symbol, while an NFA (Nondeterministic Finite Automaton) can have multiple transitions or none.
Why are DFAs preferred in lexical analysis?
+DFAs are preferred due to their deterministic nature, which ensures efficient and unambiguous tokenization of source code.
How can I minimize a DFA?
+DFA minimization can be achieved using algorithms like Hopcroft’s algorithm, which merges equivalent states to reduce the automaton’s size.
Keywords/Titles: Deterministic Finite Automata, DFA Minimization, Automata Theory, Lexical Analysis, Pattern Matching, Compiler Design.



