Understanding the Charging Capacitor Equation: A Quick Guide

Understanding the charging capacitor equation is essential for anyone working with electrical circuits. Whether you're a student, hobbyist, or professional engineer, grasping this concept simplifies circuit analysis and design. The equation describes how a capacitor charges in an RC (resistor-capacitor) circuit, providing insights into voltage, time, and capacitance relationships. This guide breaks down the equation into digestible parts, ensuring you can apply it confidently in practical scenarios. (charging capacitor equation, RC circuit, capacitor charging)
What is the Charging Capacitor Equation?
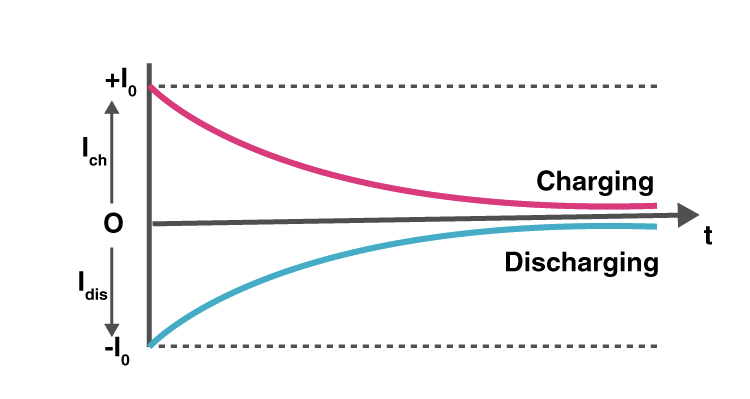
The charging capacitor equation is a fundamental formula in electronics, derived from the behavior of capacitors in RC circuits. It describes the voltage across a capacitor as it charges over time. The equation is:
VC(t) = VS (1 - e-t/RC)
Where:
- VC(t): Voltage across the capacitor at time *t*
- VS: Supply voltage
- t: Time in seconds
- R: Resistance in ohms
- C: Capacitance in farads
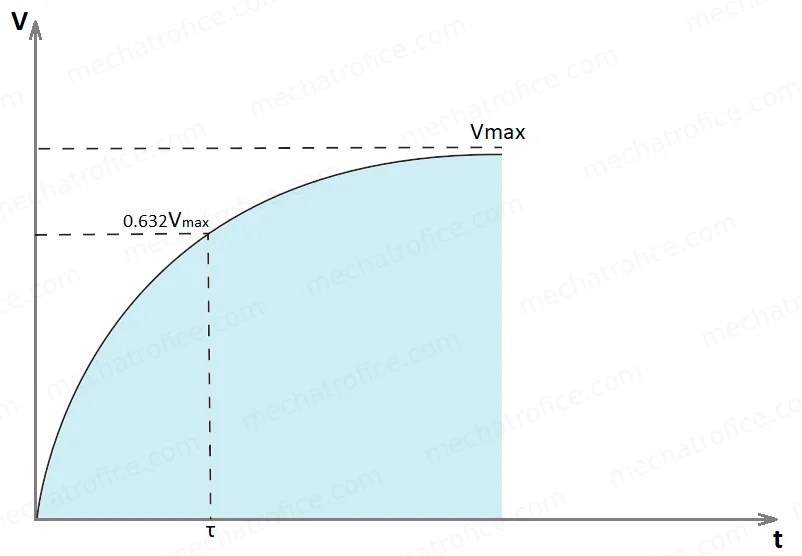
💡 Note: The time constant (τ) is given by *τ = RC*, representing the time it takes for the capacitor to charge to approximately 63.2% of the supply voltage.
Key Components of the Charging Capacitor Equation

1. Time Constant (τ)
The time constant (τ) is a critical parameter in the charging process. It determines how quickly the capacitor charges. A larger time constant means slower charging, while a smaller one results in faster charging. (time constant, capacitor charging speed)
2. Exponential Charging Behavior
The capacitor charges exponentially, meaning the rate of charging decreases over time. Initially, the voltage rises rapidly, but it gradually approaches the supply voltage asymptotically. (exponential charging, capacitor voltage)
How to Apply the Charging Capacitor Equation
Applying the equation involves a few straightforward steps:
- Identify the values: Determine the supply voltage (*VS*), resistance (*R*), capacitance (*C*), and time (*t*).
- Calculate the time constant: Use *τ = RC* to find the time constant.
- Plug into the equation: Substitute the values into the charging capacitor equation to find *VC(t)*.
Practical Applications of the Charging Capacitor Equation

This equation is widely used in various applications, including:
- Designing timing circuits in electronics.
- Analyzing power supply filters for ripple reduction.
- Understanding signal processing in communication systems.
Checklist for Applying the Charging Capacitor Equation
- Verify component values (R, C, VS) for accuracy.
- Calculate the time constant (τ) before solving the equation.
- Ensure units are consistent (e.g., seconds for time, farads for capacitance).
- Double-check calculations for exponential terms.
Mastering the charging capacitor equation empowers you to analyze and design circuits with precision. By understanding its components and applications, you can tackle complex problems in electronics and beyond. Remember, practice makes perfect—apply this equation in real-world scenarios to solidify your knowledge. (charging capacitor equation, circuit design, electronics)
What is the charging capacitor equation used for?
+
The charging capacitor equation is used to calculate the voltage across a capacitor as it charges in an RC circuit. It’s essential for circuit analysis, timing circuit design, and understanding energy storage in capacitors.
How do I calculate the time constant (τ) in an RC circuit?
+
The time constant (τ) is calculated using the formula τ = RC, where R is the resistance in ohms and C is the capacitance in farads.
Why does a capacitor charge exponentially?
+
A capacitor charges exponentially due to the nature of the RC circuit. As the capacitor charges, the voltage across it increases, reducing the current flow, which slows down the charging process over time.



