Mastering Cubic Polynomial Factorisation: A Step-by-Step Guide
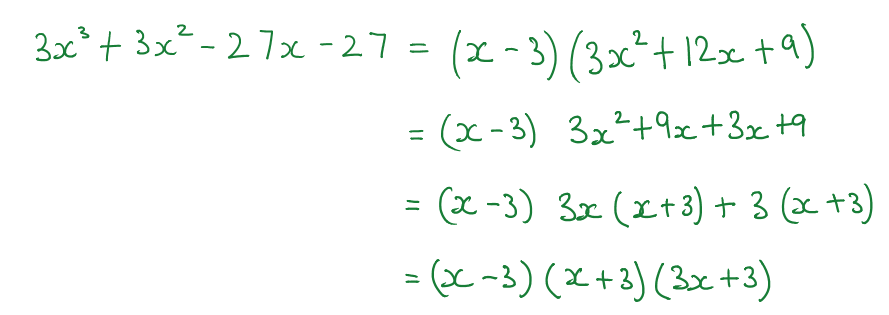
Factoring cubic polynomials can seem daunting, but with the right approach, it becomes a manageable task. Whether you're a student preparing for exams or a professional needing to brush up on algebraic skills, mastering cubic polynomial factorisation is essential. This guide breaks down the process into simple, actionable steps, ensuring you can tackle any cubic polynomial with confidence. By the end of this post, you’ll have a clear understanding of the techniques and tools needed to factorise cubic polynomials efficiently, polynomial equations,cubic equations,algebraic factorisation.
Understanding Cubic Polynomials
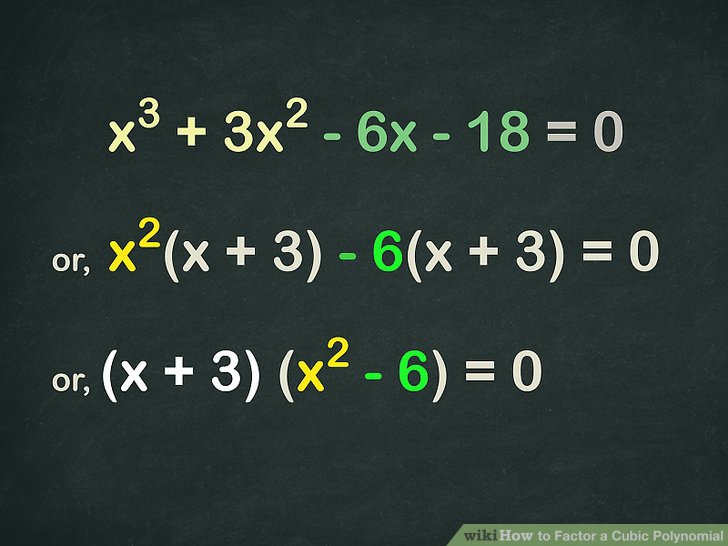
A cubic polynomial is an algebraic expression of the form ( ax^3 + bx^2 + cx + d ), where ( a ), ( b ), ( c ), and ( d ) are constants, and ( a \neq 0 ). Factoring such polynomials involves breaking them down into simpler expressions, often linear or quadratic factors. This process is crucial in solving polynomial equations and understanding their roots, cubic equations,algebraic factorisation,polynomial roots.
Step-by-Step Guide to Cubic Polynomial Factorisation

Step 1: Identify the Polynomial
Start by writing down the cubic polynomial clearly. For example, ( x^3 - 6x^2 + 11x - 6 ). Ensure you understand the coefficients and their roles, polynomial equations,cubic equations,algebraic factorisation.
Step 2: Check for Rational Roots
Use the Rational Root Theorem to test possible rational roots. These are factors of the constant term (( d )) divided by factors of the leading coefficient (( a )). For the example above, possible roots include ( \pm1, \pm2, \pm3, \pm6 ), polynomial roots,rational roots,theorem application.
Step 3: Apply Synthetic Division
Once a potential root is identified, use synthetic division to divide the polynomial by ( (x - r) ), where ( r ) is the root. This simplifies the cubic polynomial into a quadratic expression, synthetic division,polynomial division,algebraic simplification.
| Step | Description |
|---|---|
| 1 | Write coefficients of the polynomial. |
| 2 | Bring down the leading coefficient. |
| 3 | Multiply and add to find the next coefficient. |
| 4 | Repeat until all coefficients are processed. |

Step 4: Factor the Quadratic
After synthetic division, factor the resulting quadratic equation using methods like the quadratic formula or factoring techniques. This completes the factorisation of the cubic polynomial, quadratic factorisation,quadratic formula,algebraic techniques.
📌 Note: Always double-check your work by multiplying the factors to ensure they yield the original polynomial.
Tips for Mastering Cubic Polynomial Factorisation
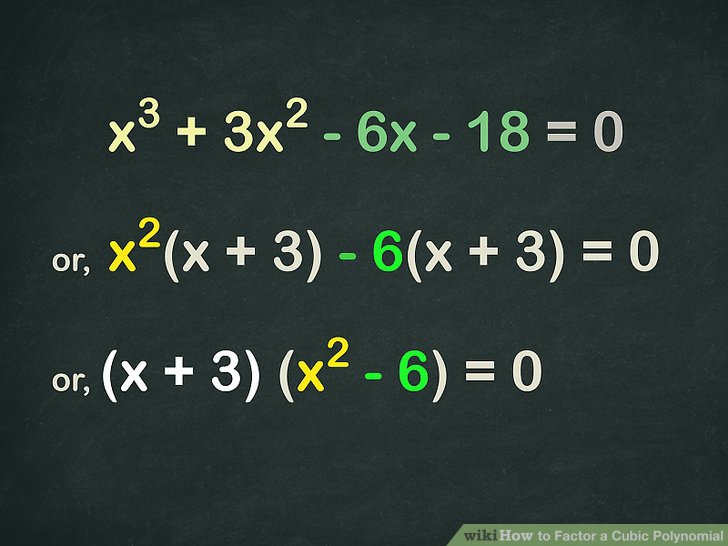
- Practice Regularly: Consistent practice improves speed and accuracy.
- Use Technology: Tools like graphing calculators can verify your results.
- Understand Patterns: Recognize common patterns in cubic polynomials for quicker factorisation.
Summary Checklist

- Identify the cubic polynomial.
- Test for rational roots using the Rational Root Theorem.
- Perform synthetic division to reduce the polynomial.
- Factor the resulting quadratic equation.
- Verify your factorisation by multiplying the factors.
Mastering cubic polynomial factorisation is a valuable skill that enhances your algebraic prowess. By following this step-by-step guide, you’ll be able to tackle complex polynomials with ease. Remember, practice and patience are key to becoming proficient in this area. Keep exploring and applying these techniques to strengthen your understanding of polynomial equations,cubic equations,algebraic factorisation.
What is the Rational Root Theorem?
+
The Rational Root Theorem states that any rational root of a polynomial equation ( anx^n + a{n-1}x^{n-1} + \dots + a_1x + a_0 = 0 ) is of the form ( \frac{p}{q} ), where ( p ) is a factor of the constant term ( a_0 ) and ( q ) is a factor of the leading coefficient ( a_n ), rational roots,theorem application.
How do I perform synthetic division?
+
Synthetic division is a shorthand method for dividing a polynomial by a linear factor ( (x - r) ). Write down the coefficients of the polynomial, bring down the leading coefficient, and then multiply and add to find the next coefficients iteratively, synthetic division,polynomial division.
Can all cubic polynomials be factored?
+
Not all cubic polynomials can be factored into linear factors with rational coefficients. Some may have irrational or complex roots, requiring advanced techniques like Cardano’s formula, polynomial factorisation,complex roots,Cardano’s formula.



