Unlocking Fintie Strain Energy Conjugates: A Comprehensive Guide

Understanding finite strain energy conjugates is crucial for engineers, material scientists, and researchers working with deformable materials. This comprehensive guide breaks down the concept, its applications, and practical considerations, ensuring you grasp this fundamental principle in mechanics.
What are Finite Strain Energy Conjugates?
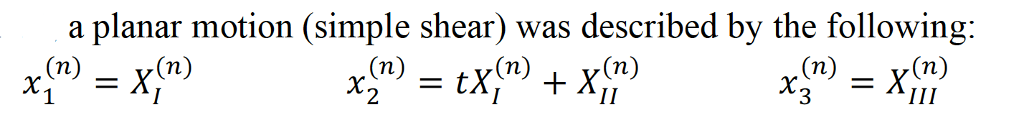
In the world of mechanics, strain energy represents the energy stored in a deformed material. Finite strain energy conjugates refer to the pairs of stress and strain measures that accurately describe this energy under large deformations. Unlike small strain theory, which simplifies calculations for minor deformations, finite strain theory is essential for understanding materials undergoing significant shape changes. Material behavior, stress analysis, finite element analysis, hyperelasticity
Why are Finite Strain Energy Conjugates Important?

Traditional small strain theory becomes inaccurate when dealing with substantial material deformations. Finite strain energy conjugates provide a more precise framework for:
- Accurate Stress Analysis: Predicting how materials behave under extreme conditions, crucial for designing structures like rubber seals, tires, and biological tissues. Stress analysis, material modeling, biomechanics
- Advanced Material Modeling: Developing realistic models for materials exhibiting nonlinear behavior, such as elastomers, polymers, and composites. Hyperelastic materials, nonlinear mechanics, material characterization
- Finite Element Analysis (FEA): Ensuring the accuracy of FEA simulations involving large deformations, leading to reliable engineering designs. FEA software, computational mechanics, structural analysis
Key Concepts: Stress and Strain Measures
Finite strain theory introduces several stress and strain measures to capture the complexities of large deformations. Common pairs of conjugates include:
- Cauchy Stress and Green-Lagrange Strain: Widely used in FEA and material modeling, offering a good balance between accuracy and computational efficiency. Cauchy stress, Green-Lagrange strain, FEA software
- 1st Piola-Kirchhoff Stress and Displacement Gradient: Suitable for analyzing materials with significant volume changes. Piola-Kirchhoff stress, displacement gradient, volumetric deformation
- 2nd Piola-Kirchhoff Stress and Green-Lagrange Strain: Preferred for isochoric (volume-preserving) deformations. 2nd Piola-Kirchhoff stress, isochoric deformation, material modeling
| Stress Measure | Strain Measure | Application |
|---|---|---|
| Cauchy Stress | Green-Lagrange Strain | General FEA, Material Modeling |
| 1st Piola-Kirchhoff Stress | Displacement Gradient | Materials with Volume Changes |
| 2nd Piola-Kirchhoff Stress | Green-Lagrange Strain | Isochoric Deformations |

Stress measures, strain measures, material behavior
Implementing Finite Strain Energy Conjugates

Incorporating finite strain energy conjugates into your analysis requires:
- Choosing the Right Conjugate Pair: Select the stress and strain measures best suited to your material and deformation type. Material properties, deformation analysis, engineering design
- Utilizing Appropriate Software: FEA software packages often offer options for different stress and strain measures. Ensure your software supports the chosen conjugate pair. FEA software, computational tools, simulation software
- Experimental Validation: Compare simulation results with experimental data to verify the accuracy of your model. Experimental testing, material characterization, validation
📌 Note: Finite strain theory can be mathematically complex. Consider consulting specialized textbooks or seeking guidance from experts in the field.
Mathematical modeling, engineering resources, technical expertiseWrapping Up

Finite strain energy conjugates are indispensable tools for accurately modeling materials undergoing large deformations. By understanding the different conjugate pairs and their applications, engineers and researchers can achieve more reliable predictions and designs. Remember, selecting the appropriate conjugate pair and utilizing suitable software are crucial for successful implementation.
What’s the difference between small strain and finite strain theory?
+Small strain theory assumes linear relationships between stress and strain, suitable for minor deformations. Finite strain theory accounts for nonlinear behavior and large deformations, providing more accurate results in such cases.
Which software supports finite strain analysis?
+Many FEA software packages, such as ABAQUS, ANSYS, and COMSOL, offer capabilities for finite strain analysis. Check the software documentation for specific details on supported stress and strain measures.
Where can I learn more about finite strain theory?
+Textbooks on continuum mechanics and nonlinear elasticity provide in-depth coverage of finite strain theory. Online resources and courses specializing in material modeling and FEA can also be valuable.



