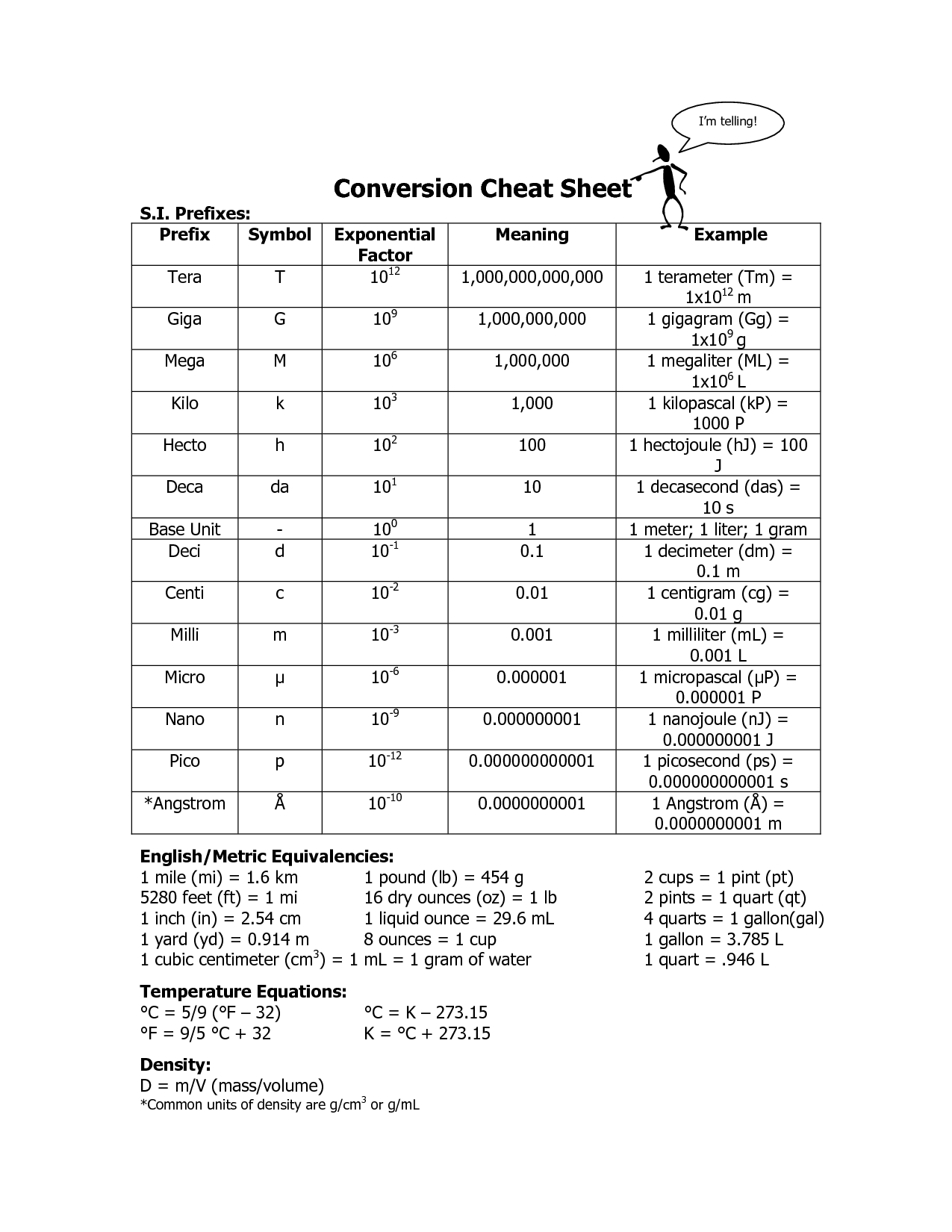
Master Factoring Binomials: Simple Steps & Examples

Factoring binomials is a fundamental skill in algebra that simplifies expressions and solves equations. Whether you're a student tackling homework or a professional refreshing your math skills, mastering this technique is essential. In this guide, we’ll break down factoring binomials into simple, actionable steps, complete with examples to ensure you grasp the concept fully. By the end, you’ll be equipped to handle any binomial factoring problem with confidence. (Factoring binomials, algebra techniques, math problem-solving)

What Are Binomials and Why Factor Them?

A binomial is a polynomial with two terms, such as ( x + 5 ) or ( 3x - 2 ). Factoring binomials involves breaking them down into simpler expressions, often using the greatest common factor (GCF) or specific formulas. This process is crucial for solving equations, simplifying expressions, and understanding more complex algebraic concepts. (Binomial definition, GCF in factoring, algebra basics)

Simple Steps to Factor Binomials

Factoring binomials doesn’t have to be daunting. Follow these steps to factor binomials efficiently:

Step 1: Identify the Binomial

Ensure the expression you’re working with has exactly two terms. For example, ( 6x + 9 ) is a binomial, while ( x^2 + 5x + 6 ) is a trinomial. (Identifying binomials, polynomial terms)

Step 2: Find the Greatest Common Factor (GCF)

Determine the GCF of the two terms. For ( 6x + 9 ), the GCF is 3. (Finding GCF, factoring techniques)

Step 3: Factor Out the GCF

Divide each term by the GCF and write the expression as a product. For ( 6x + 9 ):

( 6x ÷ 3 = 2x ) and ( 9 ÷ 3 = 3 )

So, ( 6x + 9 = 3(2x + 3) ). (Factoring out GCF, binomial factoring examples)

✨ Note: Always check if the binomial can be factored further after removing the GCF.

Examples of Factoring Binomials

Let’s apply these steps to a few examples:

Example 1: ( 10x + 15 )

1. GCF of 10x and 15 is 5.
2. Factor out 5: ( 10x ÷ 5 = 2x ) and ( 15 ÷ 5 = 3 ).
3. Result: ( 10x + 15 = 5(2x + 3) ). (Factoring examples, algebra practice)

Example 2: ( 4y - 8 )

1. GCF of 4y and 8 is 4.
2. Factor out 4: ( 4y ÷ 4 = y ) and ( 8 ÷ 4 = 2 ).
3. Result: ( 4y - 8 = 4(y - 2) ). (Binomial factoring practice, math examples)

Checklist for Factoring Binomials

• Identify if the expression is a binomial.
• Find the greatest common factor (GCF) of the terms.
• Factor out the GCF from each term.
• Write the final factored form.
• Verify your answer by distributing the GCF back into the expression. (Factoring checklist, algebra tips)

Mastering factoring binomials is a valuable skill that simplifies algebraic expressions and enhances problem-solving abilities. By following the steps outlined in this guide and practicing with examples, you’ll become proficient in no time. Remember, consistency and practice are key to mastering any mathematical concept. Keep exploring and applying these techniques to build your confidence in algebra. (Algebra mastery, math skills, problem-solving techniques)