Mastering the integration of inverse trigonometric functions is a crucial skill for anyone studying calculus or preparing for advanced mathematics exams. These functions, including arcsin, arccos, and arctan, often appear in complex integrals, and understanding their properties can simplify problem-solving significantly. Whether you're a student, educator, or professional, this guide will provide you with the essential techniques and tips to tackle these integrals with confidence.
Understanding Inverse Trigonometric Functions
Inverse trigonometric functions are the inverses of the standard trigonometric functions (sine, cosine, tangent). They are used to determine the angle from a given ratio of sides in a right triangle. Common inverse trigonometric functions include:
- Arcsin (x): The angle whose sine is x.
- Arccos (x): The angle whose cosine is x.
- Arctan (x): The angle whose tangent is x.
These functions are essential in calculus, particularly when dealing with integrals that involve trigonometric expressions. (inverse trigonometric functions, calculus, integrals)
Key Techniques for Integrating Inverse Trigonometric Functions
1. Use of Substitution
One of the most effective methods for integrating inverse trigonometric functions is the substitution method. This involves identifying a suitable substitution that simplifies the integral. For example:
- For integrals involving √(a² - x²), use the substitution x = a sin(θ).
- For integrals involving √(a² + x²), use the substitution x = a tan(θ).
- For integrals involving √(x² - a²), use the substitution x = a sec(θ).
📌 Note: Always ensure the substitution is valid within the domain of the inverse trigonometric function.
2. Integration Formulas
Memorizing key integration formulas can save time and reduce errors. Here are some essential formulas:
| Integral | Result |
|---|---|
| ∫ (1 / √(1 - x²)) dx | arcsin(x) + C |
| ∫ (1 / (1 + x²)) dx | arctan(x) + C |
| ∫ (1 / |x| √(x² - 1)) dx | arccos(x) + C |
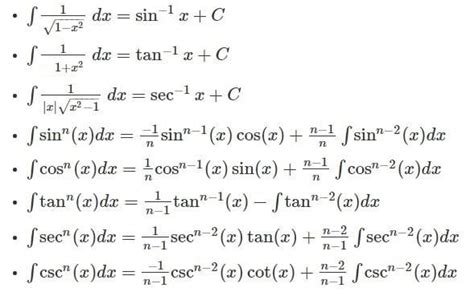
(integration formulas, substitution method, calculus techniques)
3. Practice with Examples
Practicing with examples is crucial to mastering integration techniques. Here’s a step-by-step example:
- Consider the integral ∫ (1 / √(1 - x²)) dx.
- Recognize that this matches the formula for arcsin(x).
- Apply the formula: ∫ (1 / √(1 - x²)) dx = arcsin(x) + C.
📌 Note: Always verify the solution by differentiating the result to ensure it matches the original integrand.
Mastering the integration of inverse trigonometric functions requires a solid understanding of their properties and the application of key techniques like substitution and memorized formulas. By practicing regularly and familiarizing yourself with common patterns, you can confidently tackle even the most complex integrals. Whether you're preparing for exams or advancing your mathematical skills, this guide provides the foundation you need to succeed.
What are inverse trigonometric functions?
+Inverse trigonometric functions are the inverses of sine, cosine, and tangent, used to find angles from given ratios of sides in a right triangle.
How do I choose the right substitution for integrating inverse trigonometric functions?
+Choose substitutions based on the form of the integral. For example, use x = a sin(θ) for √(a² - x²).
Why is it important to practice with examples?
+Practicing with examples helps reinforce techniques and identify patterns, making it easier to solve similar problems in the future.
