Inverse Laplace Transform of a Constant: Quick Guide

Understanding the inverse Laplace transform of a constant is essential for anyone working with Laplace transforms in mathematics or engineering. Whether you're solving differential equations or analyzing circuits, this concept simplifies complex problems into manageable forms. In this guide, we’ll break down the process step-by-step, ensuring you grasp the fundamentals and apply them effectively. By the end, you’ll have a clear understanding of how to compute the inverse Laplace transform of a constant, along with practical tips and common applications. (Laplace transform, inverse Laplace transform, constant function)

What is the Inverse Laplace Transform of a Constant?

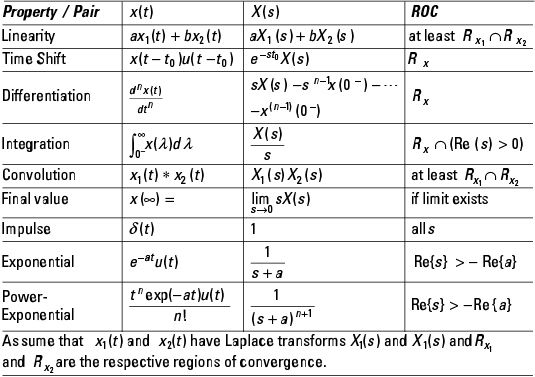
The inverse Laplace transform is a mathematical operation that converts a function from the s-domain (frequency domain) back to the time domain. When dealing with a constant function, the process becomes particularly straightforward. A constant function in the s-domain, denoted as ( F(s) = A ), where ( A ) is a constant, has a specific inverse transform that is easy to compute. This is a foundational concept in Laplace transform theory and is widely used in solving ordinary differential equations (ODEs) and analyzing systems in control theory. (Laplace transform properties, constant function, time domain)

Step-by-Step Calculation of the Inverse Laplace Transform of a Constant

To find the inverse Laplace transform of a constant ( F(s) = A ), follow these steps:

1. Identify the Constant: Ensure the function in the s-domain is a constant, i.e., ( F(s) = A ).


2. Apply the Formula: Use the standard formula for the inverse Laplace transform of a constant:
   [
   f(t) = \mathcal{L}^{-1}{A} = A \cdot \delta(t)
   ]
   where ( \delta(t) ) is the Dirac delta function.


3. Interpret the Result: The result ( f(t) = A \cdot \delta(t) ) indicates an impulse of magnitude ( A ) at ( t = 0 ).

📌 Note: The Dirac delta function is a generalized function used to model instantaneous impulses.

Practical Applications of the Inverse Laplace Transform of a Constant

The inverse Laplace transform of a constant has numerous applications across engineering and physics. Here are a few examples:

• Circuit Analysis: Used to model sudden voltage or current changes in electrical circuits.


• Control Systems: Helps analyze the response of systems to instantaneous inputs.


• Signal Processing: Applied in filtering and transforming signals with impulsive components.

Understanding this concept allows engineers and mathematicians to solve real-world problems efficiently. (Circuit analysis, control systems, signal processing)

Common Mistakes to Avoid

When working with the inverse Laplace transform of a constant, be mindful of these pitfalls:

• Mistaking the constant for a polynomial function.


• Ignoring the Dirac delta function in the result.


• Misinterpreting the physical meaning of the impulse response.

⚠️ Note: Always verify the domain of the function before applying the inverse Laplace transform.

Summary Checklist

Here’s a quick checklist to ensure you’ve mastered the inverse Laplace transform of a constant:

• Identify the constant function ( F(s) = A ).


• Apply the formula ( f(t) = A \cdot \delta(t) ).


• Understand the physical interpretation of the result.


• Avoid common mistakes in calculation and interpretation.

In summary, the inverse Laplace transform of a constant is a fundamental concept with wide-ranging applications. By following the steps outlined in this guide, you can confidently compute and interpret the results. Whether you're solving differential equations or analyzing systems, this knowledge will prove invaluable in your mathematical and engineering endeavors. (Inverse Laplace transform, constant function, Dirac delta function)