Average Explained: Mean vs. Median - Which is Correct?

When analyzing data, understanding the concept of average is crucial. However, the term “average” can be misleading, as it often refers to two distinct measures: mean and median. Both are central tendencies, but they serve different purposes and are calculated differently. This post will explore the differences between mean vs. median, their applications, and when to use each.
What is the Mean?

The mean is the most commonly used measure of average. It is calculated by summing all values in a dataset and dividing by the number of values. For example, if you have the numbers 10, 20, 30, 40, and 50, the mean is:
(10 + 20 + 30 + 40 + 50) / 5 = 30.
When to Use the Mean
- Normally Distributed Data: The mean is ideal when data follows a normal distribution (bell curve).
- Continuous Data: It works well with continuous variables like height, weight, or temperature.
- No Outliers: The mean is sensitive to outliers, so use it when outliers are not a concern.
📊 Note: The mean provides a balanced measure but can be skewed by extreme values.
What is the Median?
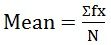
The median is the middle value in a dataset when it is ordered from lowest to highest. For the same dataset (10, 20, 30, 40, 50), the median is 30. If the dataset has an even number of values, the median is the average of the two middle numbers.
When to Use the Median
- Skewed Data: The median is better for skewed distributions where outliers exist.
- Ordinal Data: It is suitable for ordinal (ranked) data, such as survey responses.
- Robustness: The median is less affected by extreme values, making it a more reliable measure in certain cases.
🔍 Note: The median is a better choice when dealing with datasets containing outliers.
Mean vs. Median: Key Differences

To summarize, here’s a comparison table:
| Aspect | Mean | Median |
|---|---|---|
| Calculation | Sum of values / Number of values | Middle value in ordered dataset |
| Sensitivity to Outliers | High | Low |
| Best Use Case | Normally distributed data | Skewed or ordinal data |

Choosing Between Mean and Median

Deciding between mean vs. median depends on your data and goals. Here’s a quick checklist:
- Is your data normally distributed? Use the mean.
- Are there outliers in your dataset? Opt for the median.
- Are you working with ordinal data? The median is more appropriate.
For commercial-intent visitors, understanding these measures can help in making informed decisions, such as analyzing sales data or customer feedback. For informational-intent audiences, this knowledge is essential for statistical analysis and research.
What is the main difference between mean and median?
+The mean is the sum of values divided by the count, while the median is the middle value in an ordered dataset.
When should I use the median instead of the mean?
+Use the median when dealing with skewed data or outliers, as it is less sensitive to extreme values.
Can the mean and median be the same?
+Yes, in a perfectly symmetrical distribution, the mean and median are equal.
In summary, both mean and median are valuable tools for understanding data, but their application depends on the dataset’s characteristics. By choosing the right measure, you can ensure accurate and meaningful insights. Whether you’re analyzing sales trends or conducting research, knowing when to use mean vs. median is essential for data-driven decision-making. (data analysis,statistics,central tendency)