Understanding the Laplace Transform of a Constant

Understanding the Laplace Transform of a Constant is essential for anyone diving into the world of differential equations and signal processing. The Laplace Transform simplifies complex problems by converting them into algebraic equations, making it a powerful tool in engineering and mathematics. Whether you're a student, researcher, or professional, grasping this concept will enhance your problem-solving skills. In this post, we’ll break down the Laplace Transform of a constant, its applications, and why it matters, ensuring you gain a clear and practical understanding. (Laplace Transform, Differential Equations, Signal Processing)
What is the Laplace Transform?

The Laplace Transform is a mathematical technique used to transform a function of time into a function of complex frequency. It is defined as:
[ \mathcal{L}{f(t)} = F(s) = \int_{0}^{\infty} e^{-st} f(t) \, dt ]
This transform is particularly useful for solving linear differential equations with constant coefficients. By converting time-domain functions into the frequency domain, it simplifies analysis and solution processes. (Laplace Transform, Frequency Domain, Differential Equations)
Laplace Transform of a Constant

When dealing with a constant function, ( f(t) = A ), where ( A ) is a real number, the Laplace Transform simplifies significantly. The formula for the Laplace Transform of a constant is:
[ \mathcal{L}{A} = \frac{A}{s} ]
This result is derived from the integral definition of the Laplace Transform. Let’s break it down step-by-step:
- Step 1: Substitute ( f(t) = A ) into the Laplace Transform formula.
- Step 2: Evaluate the integral ( \int_{0}^{\infty} e^{-st} A \, dt ).
- Step 3: Simplify to obtain ( \frac{A}{s} ).
📘 Note: The Laplace Transform of a constant is only valid for ( s > 0 ), ensuring convergence of the integral. (Laplace Transform of a Constant, Integral Calculus)
Applications of the Laplace Transform of a Constant

The Laplace Transform of a constant has practical applications in various fields, including:
- Electrical Engineering: Analyzing circuits with DC sources.
- Control Systems: Modeling steady-state behavior of systems.
- Physics: Solving problems involving constant forces or inputs.
Understanding this concept allows engineers and mathematicians to tackle real-world problems efficiently. (Electrical Engineering, Control Systems, Physics)
Key Takeaways and Checklist
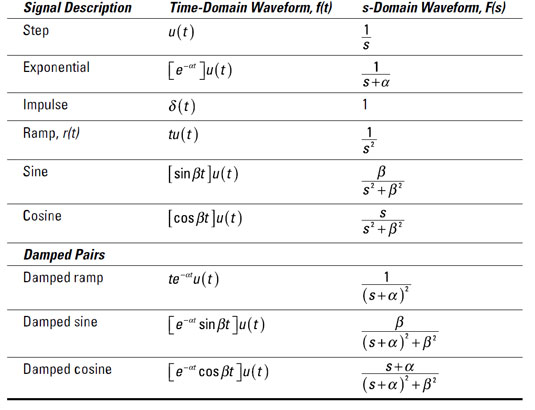
To summarize, here’s what you need to remember about the Laplace Transform of a constant:
- The Laplace Transform of a constant ( A ) is ( \frac{A}{s} ).
- It is derived from the integral definition of the Laplace Transform.
- Applications include circuit analysis, control systems, and physics problems.
Checklist for mastering the Laplace Transform of a constant:
- Understand the integral definition of the Laplace Transform.
- Practice deriving ( \mathcal{L}{A} = \frac{A}{s} ).
- Explore real-world applications in engineering and physics.
(Laplace Transform, Integral Definition, Real-World Applications)
Mastering the Laplace Transform of a constant is a foundational step in understanding more complex transforms and their applications. By breaking down the concept into manageable parts, you can build a strong foundation for tackling advanced problems in mathematics and engineering. Keep practicing, and soon you’ll find this tool indispensable in your work. (Mathematics, Engineering, Problem-Solving)
What is the Laplace Transform used for?
+
The Laplace Transform is used to solve differential equations, analyze circuits, and model systems in engineering and physics. (Laplace Transform, Differential Equations)
Why is the Laplace Transform of a constant ( \frac{A}{s} )?
+
It is derived from the integral definition of the Laplace Transform by substituting ( f(t) = A ) and evaluating the integral. (Laplace Transform of a Constant, Integral Calculus)
What are the practical applications of the Laplace Transform of a constant?
+
It is used in analyzing DC circuits, control systems, and physics problems involving constant inputs. (Electrical Engineering, Control Systems)



