Ratio Test for Series Convergence Explained Simply
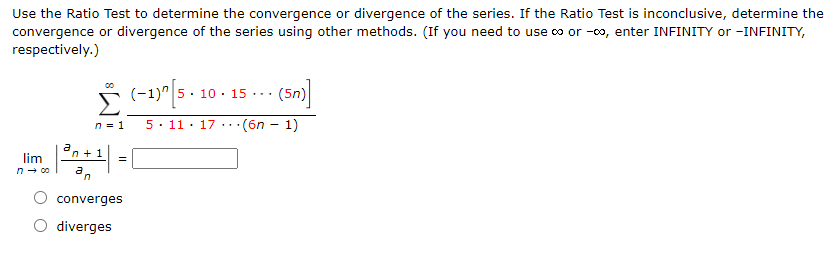
Understanding the Ratio Test for Series Convergence is crucial for anyone studying calculus or advanced mathematics. This test helps determine whether a series converges or diverges by analyzing the ratio of consecutive terms. Whether you’re a student, educator, or simply curious about mathematical concepts, this guide breaks down the Ratio Test into simple, actionable steps.
What is the Ratio Test for Series Convergence?

The Ratio Test is a method used to determine the convergence or divergence of an infinite series. It’s particularly useful for series involving complex terms like factorials, exponentials, or powers. The test compares the ratio of successive terms to assess the series’ behavior as it progresses.
How Does the Ratio Test Work?
The Ratio Test involves calculating the limit of the absolute value of the ratio of consecutive terms:
[
\lim{n \to \infty} \left| \frac{a{n+1}}{a_n} \right| = L
]
Based on the value of ( L ):
- If ( L < 1 ), the series converges.
- If ( L > 1 ), the series diverges.
- If ( L = 1 ), the test is inconclusive, and you’ll need another method to determine convergence.
📌 Note: The Ratio Test is especially handy for series where the n -th term involves powers, factorials, or exponentials.
Step-by-Step Guide to Applying the Ratio Test

Follow these steps to apply the Ratio Test effectively:
Step 1: Identify the Series
Start by identifying the series you want to test. For example, consider the series:
[
\sum_{n=1}^{\infty} \frac{n^2}{3^n}
]
Step 2: Find the General Term ( a_n )
Determine the general term of the series. In this case, ( a_n = \frac{n^2}{3^n} ).
Step 3: Compute the Ratio ( \frac{a_{n+1}}{a_n} )
Calculate the ratio of consecutive terms:
[
\frac{a_{n+1}}{a_n} = \frac{\frac{(n+1)^2}{3^{n+1}}}{\frac{n^2}{3^n}} = \frac{(n+1)^2}{3n^2}
]
Step 4: Evaluate the Limit
Find the limit of the ratio as ( n ) approaches infinity:
[
\lim{n \to \infty} \frac{(n+1)^2}{3n^2} = \lim{n \to \infty} \frac{n^2 + 2n + 1}{3n^2} = \frac{1}{3}
]
Step 5: Interpret the Result
Since ( L = \frac{1}{3} < 1 ), the series converges.
📌 Note: Always simplify the ratio before evaluating the limit to avoid unnecessary complexity.
When to Use the Ratio Test
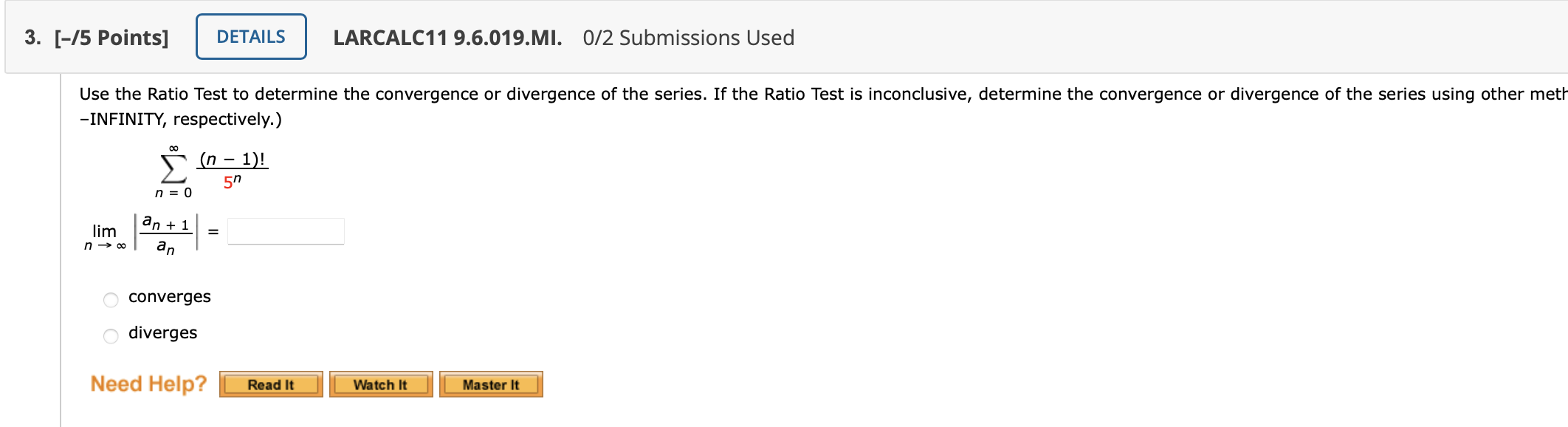
The Ratio Test is ideal for series where the terms involve:
- Exponential functions (e.g., ( a^n )).
- Factorials (e.g., ( n! )).
- Powers of ( n ) (e.g., ( n^k )).
Avoid using it for series with terms that don’t simplify easily or where the Ratio Test yields ( L = 1 ).
Checklist for Applying the Ratio Test

- Identify the series and its general term ( a_n ).
- Compute the ratio ( \frac{a_{n+1}}{a_n} ).
- Evaluate the limit as ( n ) approaches infinity.
- Interpret the result based on ( L ).
Wrapping Up

The Ratio Test is a powerful tool for determining the convergence of infinite series. By following the steps outlined above, you can confidently apply this test to a variety of series. Remember, practice is key to mastering this concept, so try applying the Ratio Test to different series to reinforce your understanding.
What is the Ratio Test used for?
+
The Ratio Test is used to determine whether an infinite series converges or diverges by analyzing the ratio of consecutive terms.
When is the Ratio Test inconclusive?
+
The Ratio Test is inconclusive when the limit ( L = 1 ). In such cases, another test is needed to determine convergence.
Can the Ratio Test be used for all series?
+
No, the Ratio Test works best for series involving terms with exponentials, factorials, or powers. It may not be effective for series with simpler terms.



