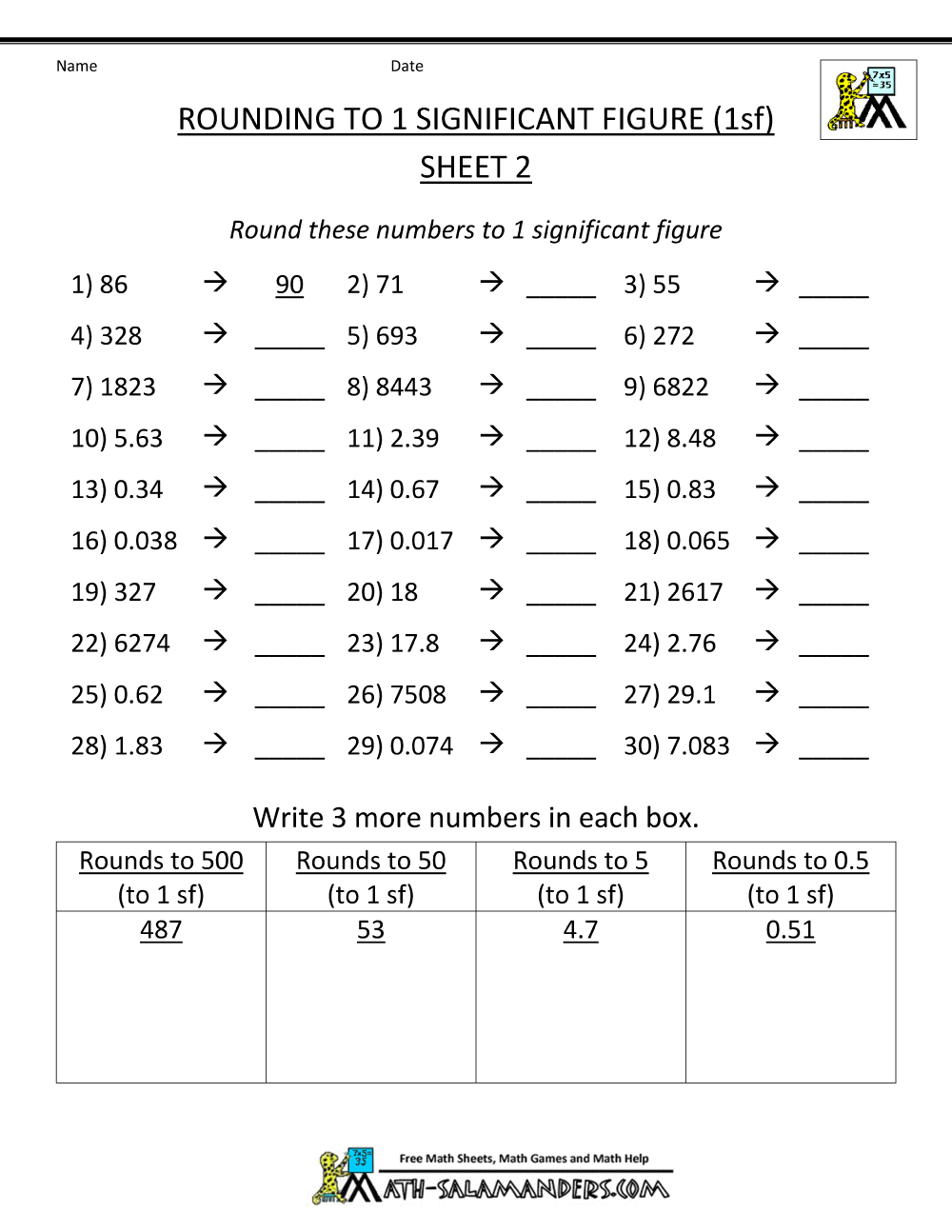
Master Significant Figures: Quick Practice Tips for Accuracy

<!DOCTYPE html>
Mastering significant figures is essential for anyone working with measurements in science, engineering, or mathematics. Whether you’re a student or a professional, understanding how to handle significant figures ensures accuracy and precision in your calculations. This guide provides quick practice tips to help you master significant figures effortlessly, enhancing your confidence in numerical work. (significant figures, accuracy in measurements, scientific calculations)
Understanding Significant Figures Basics

Significant figures are the digits in a number that carry meaning contributing to its precision. They include all certain digits and the first uncertain or estimated digit. For example, in the number 3.1415, all five digits are significant. Grasping this concept is the first step toward mastering significant figures. (significant figures definition, precision in numbers)
Rules for Identifying Significant Figures
Identifying significant figures correctly is crucial. Here are the key rules:
- Non-zero digits are always significant.
- Zeros between non-zero digits are significant.
- Leading zeros are never significant.
- Trailing zeros in a number without a decimal point are ambiguous; use scientific notation for clarity.
💡 Note: Always consider the context of the number when determining significant figures. (significant figures rules, identifying significant digits)
Practicing Significant Figures in Calculations
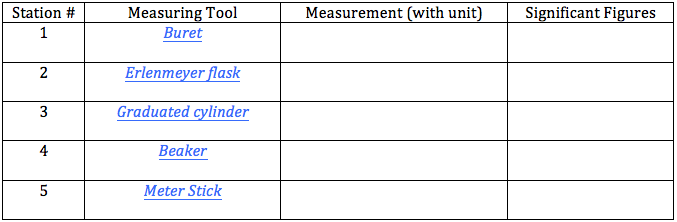
Applying significant figures in calculations ensures your results are as precise as your measurements. Follow these steps:
- Addition and Subtraction: The result should have the same number of decimal places as the measurement with the fewest decimal places.
- Multiplication and Division: The result should have the same number of significant figures as the measurement with the fewest significant figures.
| Operation | Rule |
|---|---|
| Addition/Subtraction | Fewest decimal places |
| Multiplication/Division | Fewest significant figures |

📌 Note: Consistency in applying rules is key to accurate results. (significant figures in calculations, mathematical precision)
Quick Practice Tips for Mastery

To master significant figures, practice is essential. Here are some quick tips:
- Daily Exercises: Dedicate 10 minutes daily to solving significant figure problems.
- Real-World Applications: Apply significant figures to real-life scenarios, like measuring ingredients in cooking.
- Use Online Tools: Leverage online calculators and quizzes to test your skills.
Consistent practice will make handling significant figures second nature. (practice significant figures, real-world applications)
Common Mistakes to Avoid

Avoiding common pitfalls will save you time and improve accuracy. Watch out for:
- Ignoring trailing zeros in numbers without a decimal point.
- Applying the wrong rule for addition/subtraction vs. multiplication/division.
- Overestimating precision by including too many significant figures.
⚠️ Note: Double-check your work to avoid these errors. (common mistakes, accuracy tips)
Mastering significant figures is a skill that improves with practice and attention to detail. By understanding the basics, applying the rules consistently, and avoiding common mistakes, you’ll ensure accuracy in all your numerical work. Start practicing today and watch your confidence grow! (mastering significant figures, numerical accuracy)
What are significant figures?
+Significant figures are the digits in a number that contribute to its precision, including all certain digits and the first uncertain digit. (significant figures definition)
How do I determine significant figures in a number?
+Follow these rules: non-zero digits are always significant, zeros between non-zero digits are significant, leading zeros are not significant, and trailing zeros depend on the presence of a decimal point. (determining significant figures)
Why are significant figures important in calculations?
+Significant figures ensure that the precision of your results matches the precision of your measurements, maintaining accuracy in scientific and mathematical work. (importance of significant figures)


