Simpson's Rule Calculator: Accurate Integration Made Easy
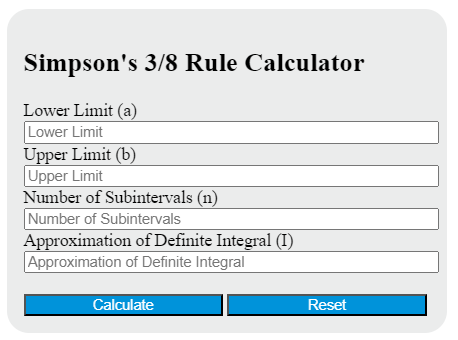
Simpson’s Rule Calculator: Simplifying Complex Integrals

Integrating functions can be a daunting task, especially when dealing with complex curves. Simpson’s Rule emerges as a powerful numerical method, offering a more accurate approximation of definite integrals compared to simpler methods like the trapezoidal rule. This blog post delves into the world of Simpson’s Rule calculators, exploring their functionality, benefits, and how they streamline the integration process. Whether you’re a student grappling with calculus or a professional engineer tackling real-world problems, understanding Simpson’s Rule calculators can significantly enhance your computational toolkit.
How Simpson’s Rule Works

Simpson’s Rule leverages parabolas to approximate the area under a curve. It divides the interval of integration into an even number of subintervals, fitting a parabola to each pair of adjacent points. This parabolic approximation provides a more precise estimate of the area compared to linear approximations. The formula for Simpson’s Rule is as follows:
| Simpson's Rule Formula |
|---|
| $\int_{a}^{b} f(x) dx \approx \frac{h}{3} [f(x_0) + 4f(x_1) + 2f(x_2) + 4f(x_3) + ... + 2f(x_{n-2}) + 4f(x_{n-1}) + f(x_n)]$ |
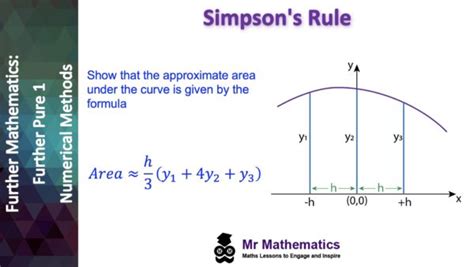
Where:
- a and b are the limits of integration.
- h is the width of each subinterval (calculated as (b - a) / n).
- n is the number of subintervals (must be even).
- xi are the points within the interval.
📝 Note: Simpson's Rule requires an even number of subintervals for accurate results.
Benefits of Using a Simpson’s Rule Calculator

Enhanced Accuracy: Simpson’s Rule calculators provide more precise approximations compared to simpler methods, especially for functions with curvature.
Time Efficiency: Calculators automate the complex calculations involved in Simpson’s Rule, saving valuable time and effort.
Error Estimation: Some advanced calculators offer error estimation features, helping you gauge the reliability of your results.
- User-Friendly Interface: Most calculators feature intuitive interfaces, making them accessible to users of all levels.
Choosing the Right Simpson’s Rule Calculator

With numerous options available, selecting the right Simpson’s Rule calculator depends on your specific needs:
Online Calculators: Convenient and readily accessible, ideal for quick calculations and learning purposes.
Software Applications: Offer more advanced features, customization options, and potentially offline functionality.
Programming Libraries: Provide flexibility and integration into larger projects for developers and researchers.
Wrapping Up

Simpson’s Rule calculators are invaluable tools for anyone dealing with numerical integration. They offer a balance between accuracy and efficiency, making complex calculations more manageable. By understanding the principles behind Simpson’s Rule and exploring the available calculator options, you can confidently tackle integration problems with greater precision and ease.
What are the limitations of Simpson's Rule?
+Simpson's Rule assumes the function is reasonably smooth within each subinterval. It may not be accurate for highly oscillating or discontinuous functions.
How does Simpson's Rule compare to the Trapezoidal Rule?
+Simpson's Rule generally provides higher accuracy than the Trapezoidal Rule, especially for functions with curvature, due to its parabolic approximation.
Can Simpson's Rule be used for improper integrals?
+Simpson's Rule can be adapted for improper integrals by using appropriate limits and potentially modifying the formula to handle singularities.
Related Keywords: Simpson’s Rule, numerical integration, definite integrals, trapezoidal rule, parabolic approximation, online calculators, integration methods, calculus tools.