Unveiling the Symmetry of Polar Equations: A Visual Guide
<!DOCTYPE html>
Polar equations offer a unique lens to explore mathematical symmetry, blending artistry with precision. Unlike Cartesian coordinates, polar equations reveal patterns that rotate, reflect, and repeat in captivating ways. This guide delves into the visual beauty and underlying principles of symmetry in polar equations, making complex concepts accessible and engaging.
Understanding Polar Coordinates and Symmetry

Polar coordinates use radius r and angle θ to plot points, creating curves that often exhibit symmetry. Symmetry in polar equations can be rotational, reflective, or point symmetry, each offering distinct visual patterns. Understanding these types is key to mastering polar graphs.
Types of Symmetry in Polar Equations
- Rotational Symmetry: Occurs when a graph repeats itself after a certain angle, like r = sin(nθ).
- Reflective Symmetry: Mirrors across the polar axis or line θ = π/2, seen in r = cos(θ).
- Point Symmetry: Exists when the graph looks the same after a 180-degree rotation, as in r = 1 + cos(θ).
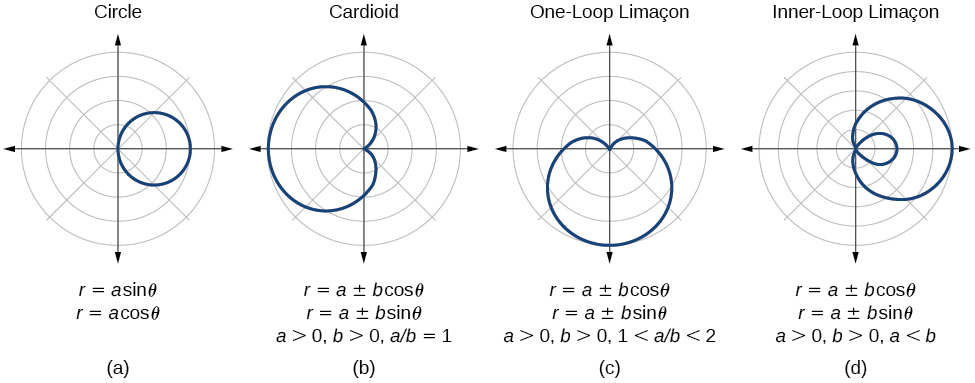
Visualizing Symmetry: Key Polar Equations

Certain polar equations are renowned for their symmetrical beauty. Below is a table showcasing examples and their symmetry types:
| Equation | Symmetry Type |
|---|---|
| r = sin(3θ) | Rotational (3-fold) |
| r = 1 + cos(θ) | Point Symmetry |
| r = 2cos(2θ) | Reflective (polar axis) |

Steps to Identify Symmetry in Polar Equations
- Plot the equation using graphing tools or manually.
- Check for repeated patterns at regular angles (rotational symmetry).
- Look for mirroring across the polar axis or θ = π/2 (reflective symmetry).
- Rotate the graph 180 degrees to test for point symmetry.
📌 Note: Symmetry identification becomes easier with practice and visualization tools like Desmos or GeoGebra.
Applications of Polar Symmetry in Real-World Scenarios

Polar symmetry isn’t just mathematically elegant—it’s practical. Applications include:
- Architecture: Designing structures with rotational symmetry, like domes.
- Engineering: Modeling spiral patterns in springs or gears.
- Art: Creating intricate designs using reflective and rotational symmetry.
Checklist for Mastering Polar Symmetry
- Learn the basics of polar coordinates and symmetry types.
- Practice plotting key polar equations like r = sin(nθ) and r = a ± bcos(θ).
- Use graphing tools to visualize and analyze symmetry.
- Explore real-world applications to deepen understanding.
By grasping the symmetry of polar equations, you unlock a world where math and art converge, offering both aesthetic pleasure and practical insights. polar coordinates,symmetry in math,visualizing equations,mathematical patterns
What is rotational symmetry in polar equations?
+Rotational symmetry occurs when a polar graph repeats itself after a specific angle, often seen in equations like r = sin(nθ).
How do I identify point symmetry in a polar graph?
+Rotate the graph 180 degrees. If it looks the same, it has point symmetry, as in r = 1 + cos(θ).
Can polar symmetry be applied outside mathematics?
+Yes, polar symmetry is used in architecture, engineering, and art to create balanced and aesthetically pleasing designs.



